Цифровые подписи, основанные на симметричных криптосистемах

Родоначальниками ЭЦП, основанной на симметричных криптосистемах стали У. Диффи и М. Хеллман, опубликовавшие описание подхода, позволяющего выполнять процедуру цифровой подписи одного бита с помощью блочного шифра.

Схема данной подписи будет следующей:

При алгоритме зашифрования Ek, оперирующий блоками данных X размера n и использующий ключ размером nk: |X|=n, |K|=nk. Структура ключевой информации в схеме следующая: секретный ключ подписи ks выбирается как произвольная (случайная) пара ключей k0, k1 используемого блочного шифра:

ks = (k0,k1);

Таким образом, размер ключа подписи равен удвоенному размеру ключа использованного блочного шифра:

|Ks| = 2|K| = 2nK.

Ключ проверки представляет собой результат шифрования двух блоков текста X0 и X1 с ключами k0 и k1 соответственно:

где являющиеся параметром схемы блоки данных несекретны и известны проверяющей подпись стороне. Таким образом, размер ключа проверки подписи равен удвоенному размеру блока использованного блочного шифра:

|kv| = 2|X| = 2n.

Алгоритм Sig выработки цифровой подписи для бита t (t {0,1}) заключается просто в выборе соответствующей половины из пары, составляющей секретный ключ подписи:

Алгоритм Ver проверки подписи состоит в проверке уравнения Ekt(Xt)=Ct, которое, очевидно, должно выполняться для нашего t. Получателю известны все используемые при этом величины.

Таким образом, функция проверки подписи будет следующей:

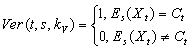
Предложенная Диффи и Хеллманом схема цифровой подписи на основе классического блочного шифра обладает такой же стойкостью, что и лежащий в ее основе блочный шифр, и при этом весьма проста. Однако, у нее есть два существенных недостатка:

    данная схема позволяет подписать лишь один бит информации. В блоке большего размера придется отдельно подписывать каждый бит, поэтому даже с учетом хэширования сообщения все компоненты подписи - секретный ключ, проверочная комбинация и подпись получаются довольно большими по размеру и более чем на два порядка превосходят размер подписываемого блока.

    пара ключей выработки подписи и проверки подписи могут быть использованы только один раз. Выполнение процедуры подписи бита сообщения приводит к раскрытию половины секретного ключа, после чего он уже не является полностью секретным и не может быть использован повторно. Поэтому для каждого подписываемого сообщения необходим свой комплект ключей подписи и проверки. Это практически исключает возможность использования рассмотренной схемы Диффи-Хеллмана в первоначально предложенном варианте в реальных системах ЭЦП.

АИСС БКБ, www.orioncom.ru, tel (495) 783-5510